期刊VIP學術指導 符合學術規范和道德
保障品質 保證專業,沒有后顧之憂
期刊VIP學術指導 符合學術規范和道德
保障品質 保證專業,沒有后顧之憂
采用蒙特卡羅抽樣與粒子模擬相結合的方法,數值研究了材料二次電子產額對腔體雙邊二次電子倍增瞬態演化及飽和特性的影響.研究發現:隨著材料二次電子產額的增加,二次電子增長率以及穩態二次電子數目和振幅均呈現增加的趨勢,放電電流起振時間逐步縮短,穩態電流幅值以及放電功率平均值和振幅值均呈現逐步增加并趨于飽和的規律,沉積功率波形延時以及脈寬呈現逐步增加并趨于飽和的趨勢.粒子模擬給出了高/低二次電子產額情況下的電子相空間分布、電荷密度分布、平均碰撞能量、平均二次電子產額、二次電子數目和放電電流的細致物理圖像.模擬結果表明:高二次電子產額材料,飽和時更傾向趨于單邊二次電子倍增類型分布;低二次電子產額材料的二次電子倍增飽和特性由空間電荷場的“去群聚”效應和“反場”效應同時決定,而高二次電子產額材料的二次電子倍增飽和特性則主要是由發射面附近的強空間電荷場“反場”效應決定的.
關鍵詞:雙邊二次電子倍增瞬態特性,材料二次電子產額,蒙特卡羅方法,粒子模擬方法;電子論文發表期刊
1引言
二次電子倍增是由二次電子驅動的一種真空共振放電現象,其可以在很多結構下產生,如:加速器、微波器件的腔體結構表面、微波輸出窗表面以及人造衛星敏感器件內部,并導致嚴重后果,包括射頻擊穿、建場失敗、沿面閃絡以及噪聲干擾等.作為一種最基本的二次電子倍增類型,金屬雙邊二次電子倍增已經得到廣泛研究.Vaughan[1]建立了細致的動力學理論分析模型并得到了聚焦相位條件;Kishek等[2]給出了共振方程并據此給出了雙邊二次電子倍增的敏感曲線;Kishek和Lau利用電子面片簡化模型研究了雙邊二次電子倍增與外電路互作用的過程[3],最近Kishek還發現并證明了ping-pong類型雙邊二次電子倍增的存在[4].
國內外許多工作都是采用基于粒子軌跡跟蹤的蒙特卡羅方法,對不同領域的二次電子倍增敏感區間進行預估和相關分析,由于蒙特卡羅方法并未考慮二次電子倍增過程中的空間電荷效應,因此無法獲得完整的物理圖像和深入認識[5−9].Gopinath等[10]首次使用粒子模擬(particle-in-cell)方法驗證了Kishek動力學理論模型所得雙平板二次電子倍增的相關規律.Riyopoulos[11]則單獨討論了空間電荷效應對雙邊二次電子倍增的影響.
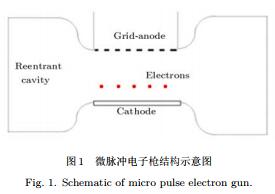
針對加速器腔體射頻建場過程[12−14]中二次電子倍增形成機理的研究需要,我們借鑒Kim和Verboncoeur[15]模擬介質窗二次電子倍增的思路,前期采用粒子模擬方法細致研究了金屬雙邊二次電子倍增的瞬態及飽和特性,給出了二次電子倍增瞬態演化及飽和過程的物理圖像[16].由于加速器腔體選用的是無氧銅材料,其材料二次電子產額系數較低(δmax0≈1.3,δmax0為材料正入射二次電子產額系數);而同樣是基于雙邊二次電子倍增機理工作的微脈沖電子槍(如圖1所示)通常選用的材料是金屬表面氧化鎂鍍膜[17],其材料二次電子產額系數極高(δmax0≈16).Buyanova等[18]研究發現:平行平板結構中若二次電子產額超過某個閾值,可能會出現兩個互不耦合的單邊二次電子倍增取代雙邊二次電子倍增的現象,但其形成機理尚不明確.
不同材料二次電子產額系數對腔體雙邊二次電子倍增的瞬態演化和飽和過程中所起的作用機理有何不同?本文在前期工作基礎之上,重點研究了腔體內表面材料的不同二次電子產額對二次電子倍增形成及飽和階段的影響過程.粒子模擬研究發現,二次電子倍增飽和階段,高/低二次電子產額材料的飽和機制有所不同,導致其表現出的物理現象不同.
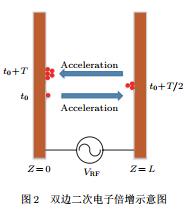
2物理建模圖2所示為腔體雙邊二次電子倍增簡化模型,腔體間距為L,初始電子在射頻電壓VRF=VRF0sin(ωt+θ0)(VRF0為幅值,ω=2πf,f為工作頻率,T為射頻周期,f=1/T,θ0為初始相位)作用下,從腔體壁面一側發射,經過半個射頻周期(主模式)后獲得能量轟擊腔體另一側壁面,激發出多于初始電子數目的二次電子,如此往復,便會出現二次電子倍增效應.當射頻場頻率、振幅以及器件結構參數達到某種匹配時,就有可能誘發雙邊二次電子倍增現象.本文采用粒子模擬與蒙特卡羅抽樣算法(抽樣二次電子的初始發射速度和角度)相結合的方法,從第一原理出發,研究與評估材料二次電子產額對腔體雙邊二次電子倍增瞬時特性的影響過程和作用機理.
2.1動力學方程與粒子模擬方法模型中考慮了射頻場與帶電粒子產生的空間電荷場對粒子的雙重作用,暫未考慮腔體加載效應的影響(即尚未考慮射頻電壓幅值VRF0與外電路聯動的動態變化).
3數值模擬結果
粒子模擬中,設置射頻頻率f=72MHz,板間距L=4cm,二次電子倍增發生面積A=1.77cm2,初始種子電子電流密度10µA/cm2(作用時間為射頻注入開始后的一個周期內,位置隨機出現在左右平板端面).由蒙特卡羅模擬得到射頻電壓幅值VRF0的二次電子倍增敏感區間(一階)為420—810V,不失一般性,設定射頻電壓幅值VRF0=550V,模擬中設置材料正入射二次電子產額最大值δmax0分別為1.3,2.0,3.0,12.0,16.0,研究不同材料的二次電子產額對金屬雙邊二次電子倍增瞬時特性的影響規律和作用機理.
首先研究不同二次電子產額材料對二次電子倍增過程中宏觀物理量瞬態演化特性的影響,包括二次電子數目、放電電流、放電功率和沉積功率等.某時刻電子數目通過對該時刻間隙空間內所有二次電子的數目累加求和獲得.某時刻放電電流采用對該時刻所有二次電子的速度與電荷量乘積累加求和后,再除以間隙長度計算獲得.放電功率通過瞬時射頻電壓與瞬時放電電流的乘積進行計算,沉積功率是時間步長內所有電子碰撞壁面損失能量除以時間步長后得到的數值.穩態階段指的是二次電子倍增的趨于飽和后的階段.
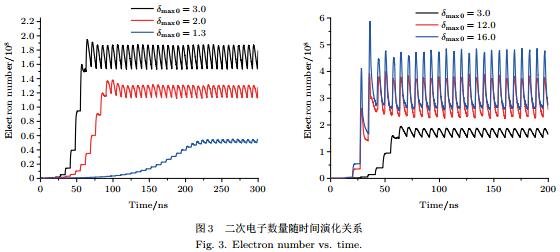
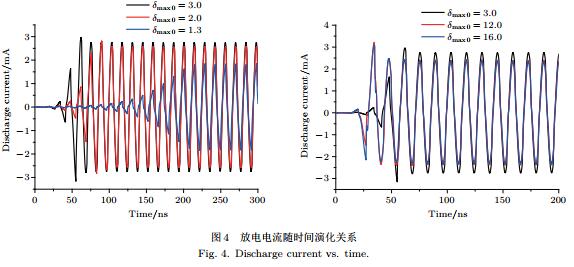
圖3和圖4分別給出了二次電子倍增瞬態演化過程中二次電子數量和放電電流隨時間的演化關系,可以看出:二次電子數目和放電電流均隨時間以指數形式快速增長后趨于飽和振蕩.二次電子倍增發展階段,二次電子數目增長率隨材料二次電子產額增長呈現增加趨勢;二次電子倍增飽和階段,飽和二次電子數目及其振幅隨材料二次電子產額增長亦呈現增加的規律.材料二次電子產額對放電電流的起振時間影響顯著,隨著材料二次電子產額的增長放電電流起振時間明顯縮短.與穩態二次電子數目不同的是,穩態電流幅值隨材料二次電子產額的增長呈現出非持續增長規律,而是逐漸增加后有所降低并趨于飽和的規律.
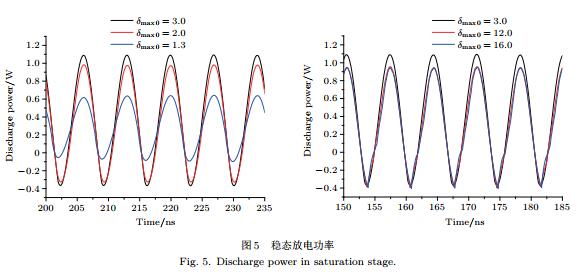
穩態放電功率波形如圖5所示,穩態放電功率存在負值,說明二次電子倍增過程中存在充電現象,即電流波形相對電壓存在延時效應.隨著材料二次電子產額的增加,放電功率呈現正向幅值和負向幅值同時增加的規律(正向幅值絕對值大于負向幅值絕對值),而后穩態放電功率有所下降并最終達到惟一的飽和值.穩態沉積功率波形如圖6所示,穩態沉積隨時間演化呈現脈沖形式,這是由二次電子倍增相位聚焦區間決定的.隨著材料二次電子產額的增加,沉積功率波形出現明顯“拖尾”現象直到趨于飽和,該現象是材料二次電子產額增加導致二次電子數目增加,引發愈發強烈的空間電荷效應所導致的.
其次,通過分析討論電子相空間、電荷密度、空間電荷場時空分布以及平均二次電子產額、平均碰撞能量、放電電流、間隙電壓與二次電子數目的相互關系,細致研究了低二次電子產額(δmax0=1.3)和高二次電子產額(δmax0=16.0)材料對二次電子倍增不同的影響過程和作用機理.
圖7和圖8分別給出了穩態時二次電子相空間和電荷密度分布狀態,可以看出:對于低二次電子產額材料,電荷密度最大值位于壁面位置附近,電子渡越過程中,電荷密度逐漸降低但空間分布逐漸變寬,這是由出射電子速度雜散效應以及空間電荷效應共同引發的,相空間上存在許多雜散的電子分布,說明穩態階段的空間電荷效應較為強烈,電子間的排斥作用較為明顯;對于高二次電子產額材料,大部分電子集中分布在腔體壁面附近,間隙內的電子渡越運動受到了明顯的抑制,間隙內未形成明顯的“空間群聚”現象,電荷密度最大值出現在金屬壁面附近并明顯高于低二次電子產額材料情況下的電荷密度最大值,間隙內部存在數值極低的電荷密度分布,表明空間電荷效應隨著材料二次電子產額的增加呈現出明顯增強的趨勢.
4結論
本文采用蒙特卡羅抽樣與粒子模擬相結合的方法,數值研究了材料二次電子產額對腔體雙邊二次電子倍增瞬態演化及飽和特性的影響.研究發現,隨著材料二次電子產額的增加,二次電子增長率以及穩態二次電子數目和振幅均呈現增加的趨勢,放電電流起振時間逐步縮短,穩態電流幅值以及放電功率的平均值和振幅值均呈現逐步增加并趨于飽和的規律,沉積功率波形延時以及脈寬呈現逐步增加并趨于飽和的趨勢.
粒子模擬細致地給出了高/低二次電子產額情況下的電子相空間分布、電荷密度分布、平均碰撞能量、平均二次電子產額、二次電子數目和放電電流的物理圖像.模擬結果表明:二次電子倍增飽和階段,高/低二次電子產額材料的物理圖像有所不同,低二次電子倍增產額材料下,間隙內電子的單向渡越“群聚”特性明顯;高二次電子倍增產額材料下,電子基本位于壁面附近,渡越運動受到了明顯的抑制.對于低二次電子產額材料,二次電子數目脈寬較寬,振蕩幅度較小,放電電流波形類似“三角波”分布;對于高二次電子產額材料,二次電子數目脈寬較窄,振蕩幅度較大,放電電流波形類似“正弦波”分布.電荷密度最大值均出現在金屬壁面附近,且高二次電子產額材料的電荷密度明顯高于低二次電子產額材料情況.
隨著材料二次電子產額的增加,雙邊二次電子倍增將會向單邊二次電子倍增類型轉變.較高的二次電子產額材料,在二次電子倍增達到飽和時更傾向趨于單邊二次電子倍增類型分布.究其作用機理,二次電子倍增過程中空間電荷場起到了兩方面作用:其一,導致電子碰撞相位發散,使電子溢出聚焦相位區間;其二,導致發射面電場呈現“反場”效應阻止二次電子的發射.低二次電子產額材料情況下,二次電子倍增的飽和特性是由空間電荷場的“去群聚”效應和“反場”效應同時決定的;而高二次電子產額材料情況下,二次電子倍增的飽和特性主要是由發射面空間電荷場的“反場”效應決定的.